CF Round #509 (Div.2) E. Tree Reconstruction

Description

1 second per test
Monocarp has drawn a tree (an undirected connected acyclic graph) and then has given each vertex an index. All indices are distinct numbers from 1 to n. For every edge e of this tree, Monocarp has written two numbers: the maximum indices of the vertices of the two components formed if the edge e (and only this edge) is erased from the tree.

Monocarp has given you a list of n−1 pairs of numbers. He wants you to provide an example of a tree that will produce the said list if this tree exists. If such tree does not exist, say so.

Input

The first line contains one integer n (2≤n≤1000) — the number of vertices in the tree.

Each of the next n−1 lines contains two integers ai and bi each (\(1<=ai<bi<=n\)) — the maximal indices of vertices in the components formed if the i-th edge is removed.

Output

If there is no such tree that can produce the given list of pairs, print "NO" (without quotes).

Otherwise print "YES" (without quotes) in the first line and the edges of the tree in the next n−1 lines. Each of the last n−1 lines should contain two integers xi and yi (1≤xi,yi≤n) — vertices connected by an edge.

Note: The numeration of edges doesn't matter for this task. Your solution will be considered correct if your tree produces the same pairs as given in the input file (possibly reordered). That means that you can print the edges of the tree you reconstructed in any order.

Examples

input

4
3 4
1 4
3 4

output

YES
1 3
3 2
2 4

input

3
1 3
1 3

output

NO

input

3
1 2
2 3

output

NO

Note

Possible tree from the first example. Dotted lines show edges you need to remove to get appropriate pairs.

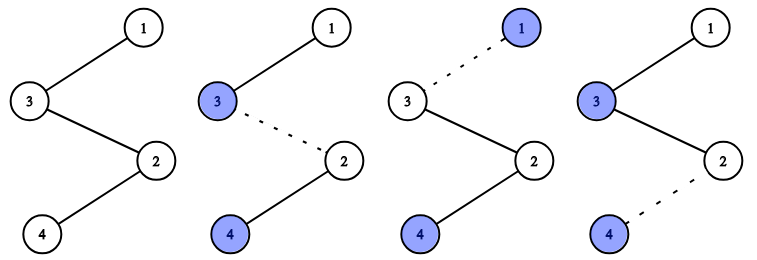
题意：
是说，要构建一个树，使得它砍掉每一条边时，左右的最大权值是给定的值。 例如样例1，4-2-3-1，砍第一二条边左右最大都是4&3，砍第三条是4&1，符合题意，然后输出每一条边的左右节点。

思路：
最最最基本的，它的某一边最大一定是n，否则直接No。 如果n，x只出现了一次，那直接n，x相连即可。 如果出现了两次，那么要在n与x中间加一个比x小的数i。 如果三次。。。 那么就直接是贪心，从最小的x开始，i也从1开始递增，根据n，x出现的次数多少决定在n，x中间加多少个数（次数-1）。

#include<bits/stdc++.h>
using namespace std;

int n,a[1010],b[1010],c[1010],now,add[1010],nown=1;

int main(){
    cin>>n;
    for(int i=1;i<n;i++){
        int x,y;
        cin>>x>>y;
        if(x==n) a[y]++;//（x,n）中x的出现次数
        else if(y==n) a[x]++; 
        else
        {
            cout<<"NO";
            return 0;
        }
    }
    int ch=1;
    for(int i=1;i<n;i++)
    {
        if(a[i])//没有就跳过
        {
            int t=n;
            while(a[i]>1&&nown<=i)//是1，直接建边
            {
                if(add[nown]==0){
                    b[++now]=t;
                    c[now]=nown;
                    add[nown]=1;
                    t=nown;
                    a[i]--;
                }
                nown++;
            }
            if(nown>i)//不是1，先往小的连，到1以后，再建边
            {
                ch=0;
                break;
            }
            b[++now]=t;
            c[now]=i;
            add[i]=1;
            a[i]--;
        }
    }
    if(ch==0)//（x,n）的次数少于剩余的小于x的数的总数了，No
    {
        cout<<"NO";
    }
    else
    {
        cout<<"YES"<<endl;
        for(int i=1;i<n;i++)
        {
            cout<<b[i]<<' '<<c[i]<<endl;
        }
    }
    return 0;
}